Copernicus: Ellipses and Circles.

Copernicus' heliocentric system exerts a clear attraction on mainstream economists' imagination. Typically, one casts oneself in the role of Copernicus, the underdog, and one's opponents as Ptolemaic astronomers/Catholic Church leaders. Things are clear: David versus Goliath.

Or, are they?

A closer look may prove instructive.


Copernicus' system had two main features: (A) the Sun is at the centre of the solar system (hence, the "-centric"), and (B) the planets orbit the Sun in circles.

Let's assume a 2D solar system and place the Sun at the origin of coordinates. Measuring distances in AU or astronomical units (1 AU = 149,597,871 km, or approximately 92.96 million miles), equation (1) below describes Earth's Copernican circular orbit :

                                 2    2
(1)                             x  + y  = 1

Graphically,

Figure 1

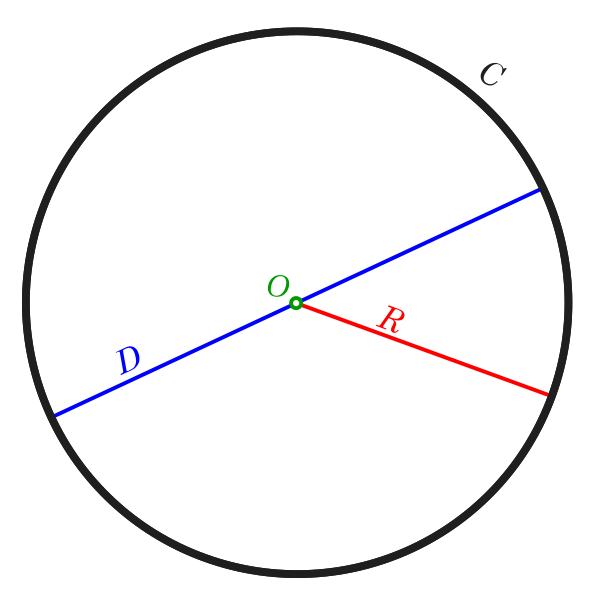[A]

The Sun goes in O, R = 1 AU.

----------

We moderns know better: Earth's orbit is an ellipse, not a circle; the Sun is not at the centre of symmetry of the ellipse, but at a focus (strictly speaking, it's not really heliocentric, but that's unimportant).

This is how an ellipse looks like

Figure 2

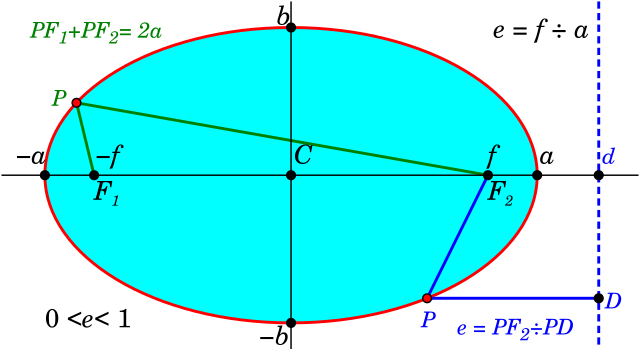[B]

Evidently, ellipses are not circles.

Placing the ellipse's centre of symmetry at the origin -- C in Figure 2 -- and the Sun arbitrarily on F1, the equation below describes Earth's orbit:

                                 2    2
                                x    y
(2)                             -- + -- = 1
                                 2    2
                                a    b

Obviously, (1) and (2) are different.

Considering things in abstract the conclusion is indisputable: Copernicus was wrong.

Take that Nick!

It seems like a clear knock out. Should we start counting to ten or call in a doctor?

----------

Not so fast. Let's try some concreteness, for a change.

Figure 3 below -- made by yours truly, using Wikipedia data, and the software GeoGebra (v. 3.2.0.0) -- represents both equations (1) and (2), making a = 1.00000261 AU and b = 0.99986297 AU in equation (2). Equation (1) is in blue; equation (2), in red.

Why 1.00000261 and 0.99986297? Because those are the actual values for Earth's orbit (interested readers are invited to check the Appendix).

Figure 3

(Right-click for an enlarged version in a new tab.)

For the purposes of graphical representation, with the software numerical calculation precision and graphical resolution available to me, both orbits are indistinguishable; the only visible -- sort of -- differences are the positions of the Sun. At the risk of stating the obvious: the deviations, which one must expect, are too small to be represented graphically.

Perhaps a more skilled analyst could have improved on that. Maybe more precise software, with higher-resolution hardware may accentuate and make more visible the differences between both curves. However, the similarity between the Copernican and Keplerian versions of Earth's orbit is undeniable. Who knew? The Earth's elliptical orbit is pretty much a perfect circle

A good comeback for a guy who was almost knocked out, eh?

----------

What does this have to do with economists and the history of economic thought? Paradoxically, Copernicus' fightback points to a weakness of Copernican economists.

You see, when it comes to knocking labour theories of value out -- Adam Smith's in this particular case -- mainstream economists love abstract reasoning, and can hardly wait to the count of ten. Concrete, numerical, empirical details be damned. Even modern day Copernicans.

We'll come back to this in the near future.

----------

Appendix.

High-school students -- or amateur astronomers -- may find this all trivial. At the other hand, who knows?

Data:
            |     km      |      AU
------------+-------------------------
Perihelion  | 147,098,291 | 0.98329134
Aphelion    | 152,098,233 | 1.01671389

Refer to equation (2). We must find a and b, using the data available.

Refer to Figure 2. To calculate a (aphelion and perihelion):

                   Aphelion + Perihelion
               a = --------------------- = 1.00000261 AU 
                            2       

Before calculating b, we'll need to find f:

                   Aphelion - Perihelion
               f = --------------------- = 0.01671127 AU 
                            2       

The Sun goes in (-f, 0) = (-0,01671127, 0).

Now, we have a and f; we must find b. We apply Pythagoras to the right triangle with sides b and f and hypotenuse a:

b = sqrt(a^2 - f^2) = 0.99986297 AU

Image Credits:
[A] "Diagram of a circle". This file was licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. Authors: DrBob, Frencheigh, Guanaco, Optimager, Jokes_Free4Me. My usage of the file does not imply anybody's endorsement of me or my usage. Source: Wikipedia.
[B] "A diagram showing some basic properties of an ellipse". This file was made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. Authors: Inductiveload, Dave3457, ElectroKid. My usage of the file does not imply anybody's endorsement of me or my usage. Source: Wikipedia.